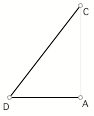
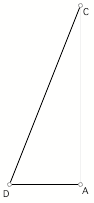
1. Measure each of these angles in radians. Record all your measurements and explain your method.

2. Remember that "cos(x)" means "the fraction of a circle's radius made by the x-coordinate of ..."

Estimate sin(CDA) and cos(CDA) directly from the triangle.

Use the methods you developed above in each of 3-6. You should be able to develop approximate answers just be producing accurate drawings and using the meanings for angle measure, sine, and cosine. Refer to this example only if you become stuck.

3. Bill crossed a river that was 100 ft. wide by heading straight across. The river swept him down stream at an angle of 35 degrees from straight across.

a) Explain how angles, angle measures, and trig functions are pertinent to this situation.

b) About how far did he have to walk up the opposite bank to stand straight across from where he started?

4. The Grand Coulee Dam is 350 ft tall. Pat, Alba, Ivonne, and Nicole got as far back from it as they could, and they still had to look up at an angle of 12 degrees from horizontal to see the top.

a) Explain how angles, angle measures, and trig functions are pertinent to this situation.

b) Approximately how far away were they from the dam?

5. Suzanne stood 250 ft from the base of a large building. She lined up a stick so that it pointed at the very top of the building. The stick made an angle of 1.2 radians with the ground.

a) Explain how angles, angle measures, and trig functions are pertinent to this situation.

b) Approximately how tall was the building?

6. Jim crossed the same river as Bill (see problem 3). The river was moving at a speed of 15 ft/sec. He could row 6 feet per second. He rowed in a direction that was straight across.

a) Explain how angles, angle measures, and trig functions are pertinent to this situation.

b) At approximately what angle from straight across the river did he end up moving?