Here is a scenario:

A high school math class is being introduced to trigonometric functions. They participated in activities involving how to measure angles. They established the convention that angles are measured by the length of a circle's arc that the angle cuts, in units of length that are proportional to the circle's circumference.

Students were given this problem to solve using just the definition of angle measure.

1. Bill crossed a river that was 100 ft. wide by heading straight across. The river swept him down stream at an angle of 35? from straight across.

How far did he have to walk up the opposite bank to stand straight across from where he started?

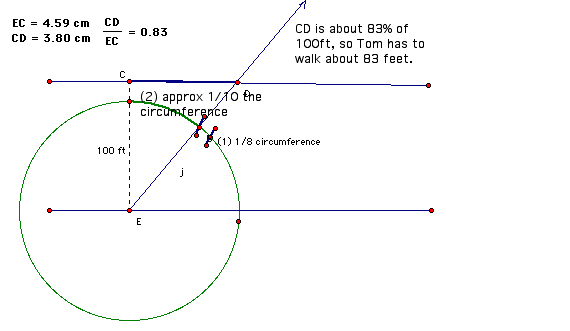
Here is one student's solution (see diagram).

35 degrees is approximately 1/10 of a circle's circumference. So I draw a circle centered at Bill's starting point, then I find 1/8 of the circle's circumference. 1/10 is 80% of 1/8, so I then found 1/10 of the circle's circumference. I drew a ray through that point on the circle, marked the intersection with the other bank, and then measured the segment that represents 100 ft and the segment that represents how far Bill had to walk. The segment that represents how far Bill had to walk is 83% as long as the segment representing the river's width, so Bill had to walk approximately 83 feet.

QUESTION: What value, if any, do you see in having students give approximate solutions to problems like this one? Why?