Do all of these problems in polar coordinates. To graph in polar coordinates in GC, type r=some expession involving theta. (Type "theta" to actually see the symbol "θ".)

1. Explain how to graph the function f(θ) = in polar coordinates, where 0 <= θ <= 2π. Then draw the graph.

2. GC continues to show the x-y coordinate plane even when you are graphing in polar coordinates. Does this matter? If so, how? If not, why?

3. Enter the function r = sin(θ). The graph appears to be a circle. How can you tell for sure?

4. The graph of r = sin(θ) in polar coordinates is a circle of diameter 1 centered at x=0, y=0.5. Is it possible for a function to have a circle of diameter 2 centered at x=0,y=0.5 as its graph in polar coordinates? Explain.

5. Enter the function y = cos(2θ), 0 <= θ <= 2π. Now do this: Construct the graph in polar coordinates by hand, with paper and pencil, using a ruler and a calculator.

Explain why the graph of y = cos(2θ) seems to "loop" four times. (Relate the behavior of cos(2θ) in polar coordinates to the behavior of cos(2x) in rectangular coordinates, where both θ and x vary from 0 to 2π radians. If you really understand your explanation, then you should also be able to explain why the graph of cos(3θ) appears to loop only three times, but really loops six times.)

Use this GC graph to investigate your functions and see them traced as θ varies from 0 to 2π radians and r varies accordingly. Just type the function definition in place of the one already there.

6. Make up a neat graph of your own to share next Monday. Why do you consider it a "neat graph"?

7. Try to make these graphs (these are all made with 0 <= θ <= 2π).

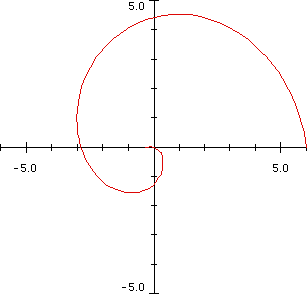
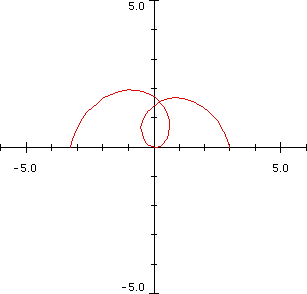
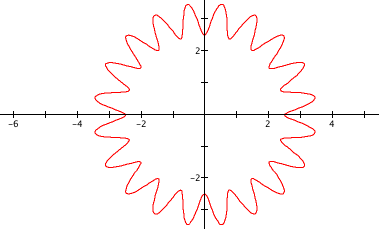
8. Use what you learned about why behaves as it does to explain why the graph of behaves as it does.