Conceptualizing Graphs

Patrick W. Thompson
Arizona State University

This assignment uses the sketch City Distances. There are two ways to use this sketch, the GSP 4.0 version or a Java version. For some reason the Java version insists on up being negative and down being positive, but it's not hard to adjust to that.

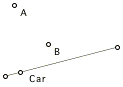
The sketch depicts a car on a stretch of road, passing between two cities named (somewhat uncreatively) City A and City B. The activities in this assignment are based on your use of that sketch.

The immediate objective is that you become able to imagine how the car's distances from the two cities vary with the car's location on the road. Subsequent objectives will be that you understand graphs with greater sophistication.

The activities in this assignment are structured in four levels. The levels begin at a level of engagement -- "making sense" of the simulation and building a strong sense of covariation (keeping track simultaneously of two quantities' values as they vary). Subsequent activities are aimed at having you be able to answer questions about covariation through your imagination.

You will be asked at times to observe, reflect, and respond to questions. When you are asked to write your answer, please include the question you are answering. This is so that when I read an answer, I know what question you are answering.

Level 1
Engagement

Move the point labeled "Car"

Watch the distances from City A and from City B as you vary the car's location

• Imagine a segment from Car to City A and observe how its length changes as the car's position varies.
• Imagine a segment from Car to City B and observe how its length changes as the car's position varies.
• Try to imagine how the two distances vary together.

Click Show Axes.

This is the set of axes on which the distances between the car and the two cities will be plotted.

Click Show A.

• Move the car.
• Watch Distance from A's behavior relative to the car's distance from an end as you move the car along the road. Keep moving the car until you understand why the distance changes as it does.

Click Hide A; then click Show B.

• Move the car.
• Watch Distance from B's behavior relative to the car's distance from an end as you move the car along the road. Keep moving the car until you understand why the distance varies as it does.

Click Show A (so that both A and B are showing)

• Move the car.
• Describe how  Distance from A and Distance from B change in relation to each other. Write your description.

Click Show Correspondence.

• What do the coordinates of Correspondence Point represent? Write your answer.

Move the car; watch Correspondence Point.

• Explain Correspondence Point's behavior with respect to the Car's location relative to the two cities as it moves along the road. Write your description.

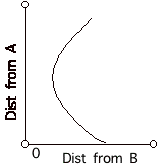
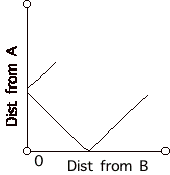
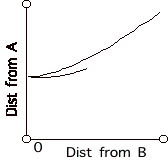
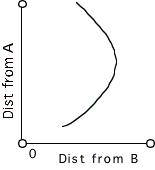
Click Show Graph.

• What information does each point on the graph give? Write your answer.
• What is the relationship between Correspondence Point and the graph? Write your answer.

Level 2
Move to Representation

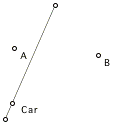
1. Here are three arrangements of the road, City A, and City B.

For each arrangement:

Imagine the behavior of Distance from A relative to the car's position as you move the car from one end of the road to the other.

Imagine the behavior of Distance from B relative to the car's position as you move the car from one end of the road to the other.

Imagine the behavior of Correspondence Point as you move the car from one end of the road to the other.

Sketch your prediction of the graph that Correspondence Point will make with this arrangment.

Test your prediction.

2. Create two arrangements that you will give to someone else. Try to make them as "tricky" as you can.

Explain why you think each will be tricky.

Level 3
Move to Reflection

1. For each graph: Locate, on paper (away from a computer), City A and City B relative to the road to produce that specific graph.

(a)		(b)
(c)		(d)

After making all your predictions:

• Test your predictions on a computer.
  • If you were way off on a graph, explain how you were thinking.
  • If you were accurate, explain as if to someone, else how to answer questions like these.

2. Make up an "impossible" City A City B graph. Explain why it is impossible.

3. Can all City A City B graphs be put into a small number of categories? What categories?

 

 

Level 4
Extending the Reflection

1. Predict what will happen to the graph as you move point B parallel to the road.

(After you have tested your prediction: Describe how the graph changes as you move point B parallel to the road. Why does the graph change as it does?)

2. Predict what will happen to the graph as you move point A perpendicular to the road.

(After you have tested your prediction: Describe how the graph changes as you move point A perpendicular to the road. Why does the graph change as it does?)

3. How would this entire set of activities change were they to involve 3 cities, A, B, and C?