Question 1
In the diagram below, angles BAC and CAD are consecutive. The term Ņrelative arcÓ means Ņthe length of the arc that the angle cuts from a circle relative to the circleÕs circumference.Ó Put another way, the term Ņrelative arcÓ means Ņthe fraction of a circleÕs circumference that the angle cutsÓ.
Josˇ measured angle BAC, getting a relative arc of 0.10. Susan measured angle CAD, getting a relative arc of 0.07. Josˇ said that angle BAD must have a relative arc of 0.17. Susan objected that you cannot simply add relative arcs, because the circles have different circumferences.
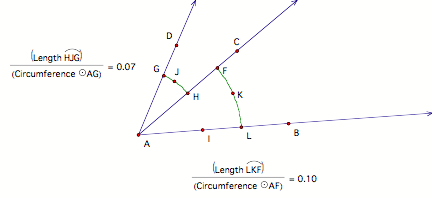
Who is correct, Josˇ or Susie? Justify your answer.
What does your answer imply about when you can add the
relative arcs of consecutive angles to get the relative arc of the angle they
form together?
Question 2
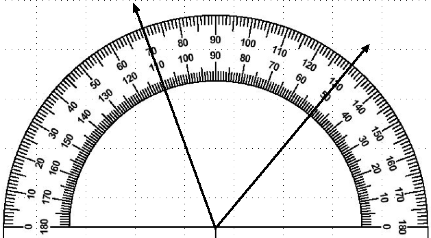
Two students in 0 hour Math 3 had this discussion:
Lisa: The angle is 0.17.
Jill: No itÕs not, itÕs
60 degrees!
Lisa: ThatÕs what I said. 60
degrees is 60/360, which reduces to 0.166666 and I rounded that to 0.17.
Jill: But that says it
is 0.17 degrees, and thatÕs a really tiny angle. And this one is not tiny.
Lisa: I didnÕt say degrees. I said
0.17, like in relative arc.
Jill: You canÕt turn a
number of degrees into relative arc! You didnÕt divide an arc length by a
circumference!
What do you
say?