
|
Ms Coombs begins this unit by guiding a
discussion about a function in factored
form. The function she chooses to use
is y=(x-1)(x-2)(x-3)(x-4). Specifically, Ms
Coombs focuses on the function outputs as
the inputs approach x=1.
|

|
Ms Coombs presents the students with a
factored form for a polynomial that includes
repeated factors: y = (x – 2)(x – 2)(x –
5)(x – 7). She does this to illuminate
that functions do not always pass through a
zero with a change in sign.
|

|
Continuing from the previous clip, Ms.
Coombs works with the given function.
Here, she allows the students to hypothesize
and refine each other’s ideas for how to
modify the question to make the function
negative on both sides of x=2. One
student tries the factors (x+2)(x+2).
Another student hypothesizes that it can
never happen.
|
|
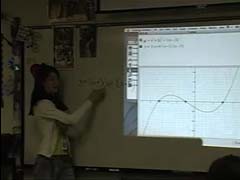
Ms Coombs has the students consider that an
alternative form for y = (x – 3)(x + 1)(x +
4) might exist. To do this, she
uses the “graphing calculator” program to
expand the factored form. The students
realize that the zeros are still present,
but not obvious, in the expanded form.
She then challenges the students to reverse
their earlier thinking and turn the graph’s
zeros into factors.
|

|
In the previous clip we saw Ms. Coombs
employ the “expand” feature on graphing
calculator. In this clip, she challenges the
students to use their earlier knowledge
about distribution to go from the factored
form to the expanded form. She uses the
function y=(x+4)(x+6) to get the students
started.
|

|
Ms. Coombs continues to lead the discussion
about a situation where Graphing Calculator
has converted the function y = (x +4)(x + 6)
to the expanded form y = x2 + 10x
+ 24. She asks students to make observations
about the connections between the two forms
with a focus on multiplication. She leads
the students to see a need to apply the
distributive property, which they studied
during the previous semester.
|

|
Ms. Coombs asks students to make a
connection between the previously learned
distributive property and the current topic
of binomial multiplication. Students assign
the placeholders a, b, and c from (a+b)c =
ac + bc to the example y = (x + 4)(x + 6).
She leads the class through the distributive
process twice in order to write the binomial
product in the expanded, quadratic form.
|

|
As part of the class work, Ms. Coombs has
the students think once again about finding
the zeros of a function in factored
form. This time, though, the factors
are not restricted to having a leading
coefficient of one. In this exchange, Ms.
Coombs works with a student to find the
zeros of y = (2x -1)(x – 4).
|
|
Prior to this clip, Ms. Coombs reviewed how
distribution expands a polynomial in
factored form. As an example, she used
y=(x+4)(x+3) to get y = x2 +
(3+4)x + (4)(3). She then directs the
students to imagine working the problem
backwards, without the aid of a graph.
The students guess as to how this may be
done.
|
|
Ms. Coombs leads the students to use the
distributive property to expand y = (x +
d)(x + e) as a way to test and generalize
their hypothesis about how to generate the
expanded form. She uses the result of this
generalization to reverse the process and
factor a quadratic polynomial.
|

|
Ms. Coombs leads the class through the
factoring of the polynomial y = x2
– 2x – 24.
|

